由华东师范大学统计学院与华东师范大学-纽约大学数学联合研究中心(上海纽约大学)共同组织的 “概率论国际研讨会:统计物理与随机矩阵”将于2025年11月1日至2日在华东师范大学中北校区举办。 本次会议旨在聚焦现代概率论及其相关领域的前沿动态,汇聚该领域的资深学者和青年研究人员,为参会者搭建一个高水平的学术交流平台,促进最新研究成果的分享、激发创新性的合作契机,并深化上海地区与国际学界之间的学术纽带。会议将涵盖现代概率论前沿的一系列广泛主题,包括交互粒子系统、统计力学、随机矩阵、随机偏微分方程等。
一、会议信息
时间: 2025年11月1日至2日
地点: 华东师范大学中北校区地理馆385室( 上海市普陀区中山北路3663号)
二 、学术委员会
Alejandro Ramírez, 上海纽约大学数学教授、数学学科负责人
俞锦炯,华东师范大学统计学院助理教授
* 按姓氏首字母排序
三、演讲嘉宾
陈鸿宾, 上海纽约大学数学助理教授
陈 昕 , 上海交通大学数学科学学院长聘副教授
何煜坤, 复旦大学上海数学中心副教授
Stefan Junk, 日本学习院大学数学助理教授
Konstantin Khanin, 北京雁栖湖应用数学研究院教授
Maximilian Nitzschner, 香港科技大学数学助理教授
夏家铭, 上海数学与交叉学科研究院助理教授
张 仑, 复旦大学数学科学学院教授
*按姓氏首字母排序
四、会议注册
会议注册系统已开通,有意参会的学者请访问会议网页进行在线注册。
https://nyu.qualtrics.com/jfe/form/SV_3DxDgmbScIxns1
联系邮箱:Shanghai.math.conference@nyu.edu 、
jjyu@sfs.ecnu.edu.cn
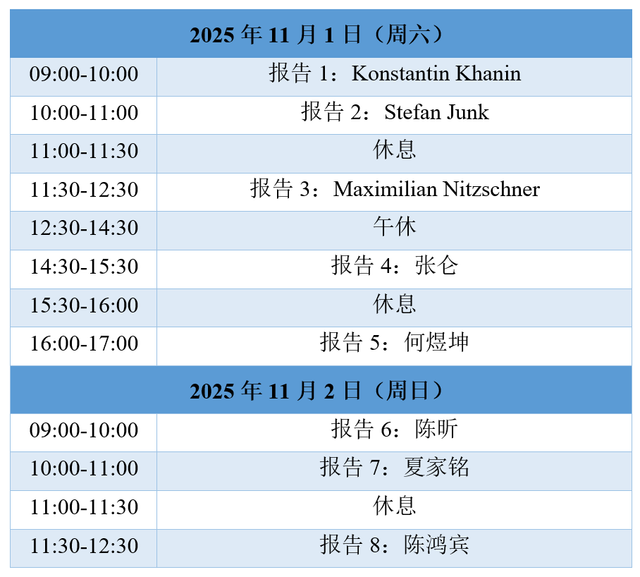
五、日程安排
六、报告摘要
1、题目:Large Deviations for The Spin-Glass Ground State
报告人:陈鸿宾 上海纽约大学
摘要:We consider the Sherrington--Kirkpatrick spin glass model and its mixed-p spin generalizations. The ground state energy is the maximum of the Hamiltonian, or the free energy when the temperature is set to be zero. The limiting ground state energy is known to be given by a Parisi-type formula. We establish the (one-sided) large deviation of this quantity by computing explicitly the limiting cumulant generating function. We also obtain an explicit variational formula for the rate function. There is also recent interest in understanding the algorithmic aspect of the ground state energy, since it is a typical optimization problem in a complex landscape. In particular, we obtain a formula for the ground state energy that is similar to the algorithmic threshold for Lipschitz algorithms. This is based on a joint work in preparation with Alice Guionnet, Justin Ko, Bertrand Lacroix-A-Chez-Toine, and Jean-Christophe Mourrat.
2、题目:Extremal Eigenvectors of Sparse Random Matrices
报告人:何煜坤 复旦大学
摘要:We consider a class of sparse random matrices, which includes the adjacency matrix of Erdős-Rényi graph. When $p\geq N^{-1+o(1)}$, we show that the non-trivial edge eigenvectors are asymptotically jointly normal. The main ingredient of the proof is a new algorithm that directly computes the joint eigenvector distributions, without comparisons with GOE. Joint work with Jiaoyang Huang and Chen Wang.
3、题目:Equivalence of Fluctuations of Discretized SHE and KPZ Equations in The Subcritical Weak Disorder Regime
报告人:Stefan Junk日本学习院大学
摘要:We study the fluctuations of discretized versions of the stochastic heat equation (SHE) and the Kardar-Parisi-Zhang (KPZ) equation in spatial dimensions d >=3 in the weak disorder regime. Under appropriate rescaling, both are expected to converge in law to the Edwards-Wilkinson equation (with Gaussian or Levy noise) but this has only been shown under a sub-optimal moment condition. We show that the fluctuations of both equations are close in probability up to the critical point, which indicates that they have the same scaling limit (the existence of which remains open). The discretization is defined using the directed polymer model. Joint work with Shuta Nakajima.
4、题目:First Passage Percolation in a Product-Type Random Environment
报告人:Konstantin Khanin 北京雁栖湖应用数学研究院
摘要:We consider a first passage percolation model in dimension 1 + 1 with potential given by the product of a spatial i.i.d. potential with symmetric bounded distribution and an independent i.i.d. in time sequence of signs. We assume that the density of the spatial potential near the edge of its support behaves as a power, with exponent κ > −1. We investigate the linear growth rate of the actions of optimal point-to-point lazy random walk paths as a function of the path slope and describe the structure of the resulting shape function. It has a corner at 0 and, although its restriction to positive slopes cannot be linear, we prove that it has a flat edge near 0 if κ > 0. For optimal point-to-line paths, we study their actions and locations of favorable edges that the paths tend to reach and stay at. Under an additional assumption on the time it takes for the optimal path to reach the favorable location, we prove that appropriately normalized actions converge to a limiting distribution that can be viewed as a counterpart of the Tracy–Widom law. Since the scaling exponent and the limiting distribution depend only on the parameter κ, our results provide a description of a new universality class.
5、题目:Solidification Estimates for Random Walks on Supercritical Percolation Clusters
报告人:Maximilian Nitzschner 香港科技大学
摘要:We consider the simple random walk on the infinite cluster of supercritical Bernoulli bond percolation on the integer lattice in dimension larger or equal to three. For almost every realization of the percolation configuration, we obtain uniform bounds on the absorption probability of the walk by "porous interfaces" surrounding the discrete blow-up of a compact set. Our proof relies on a fine analysis of the regularity of heat kernels and the relative volume of the cluster over well-separated scales, allowing the construction of a "resonance set". This method is robust and also applies to the infinite cluster of various correlated percolation models in their supercritical phases. Our estimates extend previous controls obtained for Brownian motion (in a joint work with Sznitman) and for the random walk among random, uniformly elliptic conductances on the integer lattice (in a joint work with Chiarini) to a manifestly non-elliptic set-up. Such solidification-type estimates and related capacity bounds have been instrumental for proving sharp bounds for various large deviation-type problems in correlated percolation models.
Based on joint work with A. Chiarini (University of Padova) and Z. Liu (The Hong Kong University of Science and Technology).
6、题目:Computing N-Point Function in The Planar Two-State Fuzzy 4-Potts Model, via The Convergence of 6V Height Function to GFF
报告人:夏家铭 上海数学与交叉学科研究院
摘要:We consider the planar critical random cluster model on the square lattice with cluster weight q=4. On each cluster we put an independent ±1 spin with probability 1/2, resulting a particular case of fuzzy Potts models. Based on the BKW coupling between random cluster models and 6-vertex models and also based on a recent work-in-progress proving the convergence of 6-vertex height function to GFF, we show how to compute the n-point correlation function of the spin field as the mesh size vanishes, for all n.
7、题目:The Multiplicative Constant in Asymptotics of Higher-Order Analogues of The Tracy-Widom Distribution
报告人:张仑 复旦大学数学科学学院教授
摘要:In this talk, we are concerned with higher-order analogues of the Tracy-Widom distribution, which describe the eigenvalue distributions in unitary random matrix models near critical edge points. The associated kernels are constructed by functions related to the even member of the Painlev\'{e} I hierarchy $\mathrm{P_{I}^{2k}}$, and are regarded as higher-order analogues of the Airy kernel. We are able to establish the multiplicative constant in asymptotics of the distribution, resolving an open problem in the work of Clayes, Its and Krasovsky. An important new feature of the expression is the involvement of an integral of the Hamiltonian associated with a special, real, pole free solution for $\mathrm{P_{I}^{2k}}$. In addition, we show that the total integral of the Hamiltonian vanishes for all $k$, and establish a transition from the higher-order Tracy-Widom distribution to the classical one. Our approach can also be adapted to calculate similar critical constants in other problems arising from mathematical physics. Joint work with Dan Dai, Wen-Gao Long, Shuai-Xia Xu and Lu-Ming Yao.
更多会议信息可扫码登录会议网站:

