为深入探讨概率论与统计物理模型交叉领域中的关键问题和创新方法,促进我校统计及交叉学科发展,华东师范大学统计学院、北京国际数学研究中心、上海纽约大学数学系将于2025年4月13日举办“临界指数、尺度极限、普适类:来自统计物理的挑战”会议。会议将汇聚国内外概率论领域专家学者,旨在搭建一个开放的对话平台,促进概率论领域的国际学术交流与合作。
一、会议时间、地点
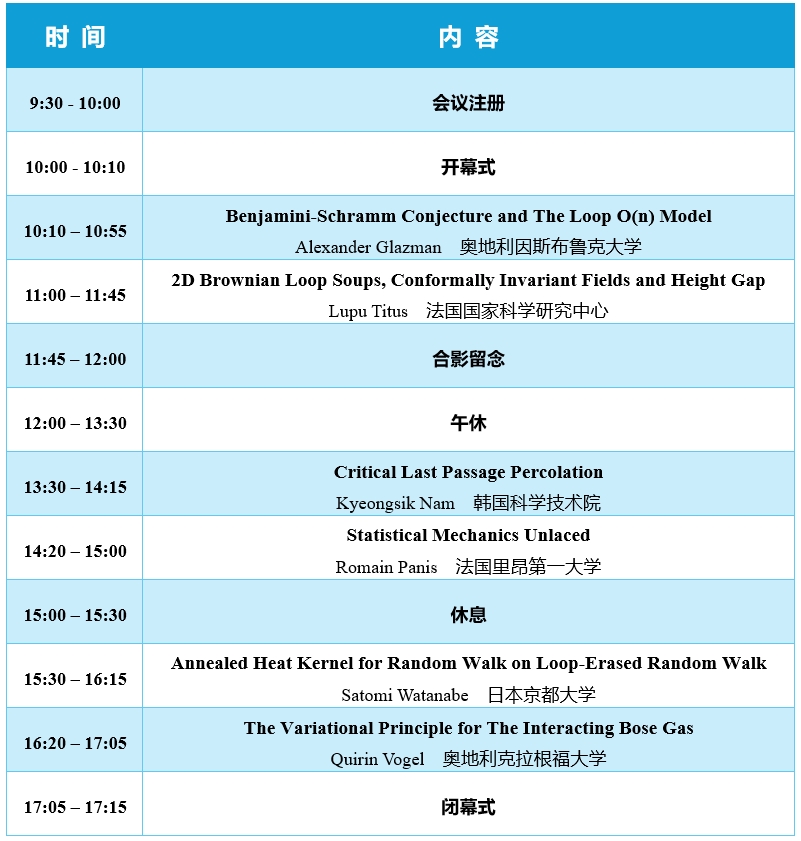
会议时间:2025年4月13日 9:30-17:30
会议地点:上海市普陀区中山北路3663号华东师范大学地理馆385教室
二、主办单位
华东师范大学统计学院
北京国际数学研究中心
上海纽约大学数学系
三、会议日程
四、报告信息
报告一:Benjamini-Schramm Conjecture and The Loop O(n) Model
摘要:We witness many phase transitions in everyday life (eg. ice melting to water). The mathematical approach to these phenomena revolves around the percolation model: given a graph, call each vertex open with probability p independently of the others and look at the subgraph induced by open vertices. Benjamini and Schramm conjectured in 1996 that, at p=1/2, on any planar graph, either there is no infinite connected components or infinitely many.
We prove a stronger version of this conjecture and use this to establish fractal macroscopic behaviour in the loop O(n) model. The latter includes a random discrete Lipschitz surface as a particular case.
Joint work with Matan Harel and Nathan Zelesko.
报告二:2D Brownian Loop Soups, Conformally Invariant Fields and Height Gap
摘要:In my talk I will present the joint work with Antoine Jego and Wei Qian, also related to earlier works with Aru and Sepulveda, as well as with Aidekon, Berestycki, Jego. The Brownian loop soups are natural Poisson collections of Brownian loops in a 2D domain, that satisfy a conformal invariance property. In particular, there is a scale invariance property with tiny loops at all small scales. The question of clusters formed by these Brownian loops hase been first studied by Sheffield and Werner. They showed a phase transition at the intensity parameter c=1. For c<= 1, the outer boundaries have been identified as Conformal Loop Ensembles CLE_k. Later, in my joint work with Aru and Sepulveda, the whole clusters at c=1 have been identified as sign components of the 2D Gaussian free field. In the work with Jego and Qian, we focus on the subcritical regime c<1. We show that the one-arm probabilities for clusters behave like | log epsilon|^{-(1-c/2)}. We further show that out of the Minkowski contents of these clusters plus some independent signs, one can construct conformally invariant random fields, which are correlated as a power of log. We prove that all these fields present a height gap phenomenon, similarly to the 2D GFF. We also formulate conjectures on the renormalized powers of these fields.
报告三:Critical Last Passage Percolation
摘要: Last passage percolation (LPP) is a model of a random metric space where the main observable is a directed path evolving in a random environment. When the environment has light tails, the fluctuations of LPP are predicted to be explained by the Kardar-Parisi-Zhang (KPZ) universality theory. However, the KPZ theory is not expected to apply for many natural environments, particularly "critical" ones exhibiting a hierarchical structure. In this talk, I will talk about such LPP with an inverse quadratic tail decay distribution which is conjectured to be the critical point for the validity of the KPZ scaling relation. As a byproduct, I will mention the resolution of a long-standing question of Martin concerning necessary and sufficient conditions for the linear growth of the LPP energy. Based on the joint work with Shirshendu Ganguly and Victor Ginsburg.
报告四:Statistical Mechanics Unlaced
摘要: Understanding the (near-)critical behaviour of lattice models is one of the main challenges in statistical mechanics. A prominent approach to this problem is the computation of the model’s critical exponents. This task is generally impossible due to the intricate interplay between the specific features of the models and the geometry of the graphs on which they are defined. A striking observation was made in the case of models defined on Z^d: beyond an upper-critical dimension d_c, the geometry no longer plays a significant role, and the critical exponents simplify, matching those found on Cayley trees or complete graphs. The regime d>d_c is called the mean-field regime of the model.
In the 1980’s, two prominent approaches have been developed to understand the mean-field regime of a wide class of models: the rigorous renormalization group method and the lace expansion. It usually requires a lot of work to transfer the analysis involved in these methods from one model to the other.
We revisit the study of the mean-field regime and present an alternative, more probabilistic, and unified approach. Our method applies to many perturbative settings including, the weakly-self avoiding walk model in dimensions d>4, spread-out Bernoulli Percolation in dimensions d>6, or even one- and two-component spin models in dimensions d>4.
Based on ongoing works with Hugo Duminil-Copin, Aman Markar, and Gordon Slade.
报告五:Annealed Heat Kernel for Random Walk on Loop-Erased Random Walk
摘要:Random walks on random graphs are associated with diffusion phenomena in disordered media. This talk focuses on the simple random walks on loop-erased random walks (LERW). We will discuss the sub-Gaussian estimate for the annealed off-diagonal heat kernel of the simple random walk on high-dimensional LERWs. In the course of the proof, we will demonstrate the Gaussian-type local central limit theorem of high-dimensional LERWs.
报告六:The Variational Principle for The Interacting Bose Gas
摘要:The Feynman representation of the interacting Bose gas is conjectured to involve “interacting interlacements” at sufficiently high densities in the thermodynamic limit, making it a challenging ensemble to study. In this talk, I will introduce the Feynman loop representation and explain how we can use it to derive a (probabilistic) variational principle for the pressure of the interacting gas at all densities. The main challenge is to piece together short snippets of paths into longer segments, using large deviation tools and point process theory. This is joint work (in progress) with G. Bellot (University of Lille).
五、联系方式
联系人:俞老师
邮 箱:jjyu@sfs.ecnu.edu.cn
